文炎同学的AI知识库

Appearance

Return to top
On this page

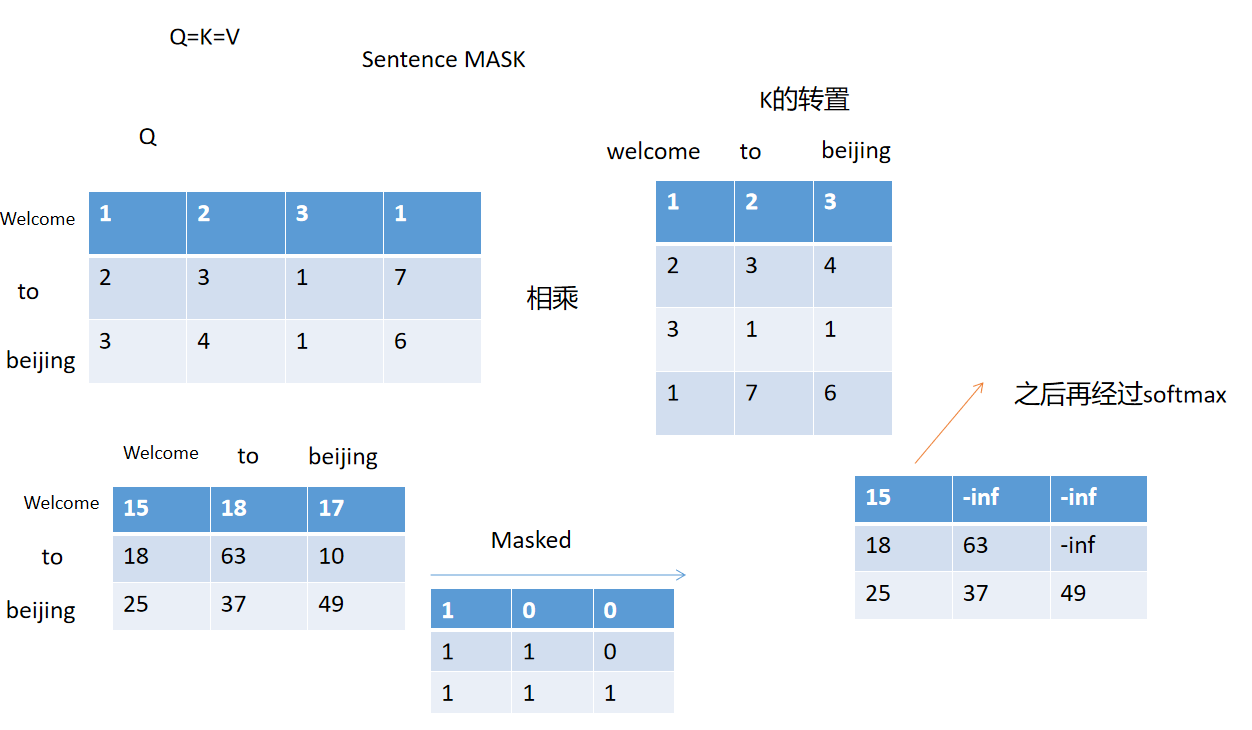
1. transformer

Transformer 是一种基于自注意力机制（Self-Attention）的深度学习模型架构，最初被设计用于解决自然语言处理（NLP）中的序列转换任务（如机器翻译）。

2. 传统seq2seq的缺点

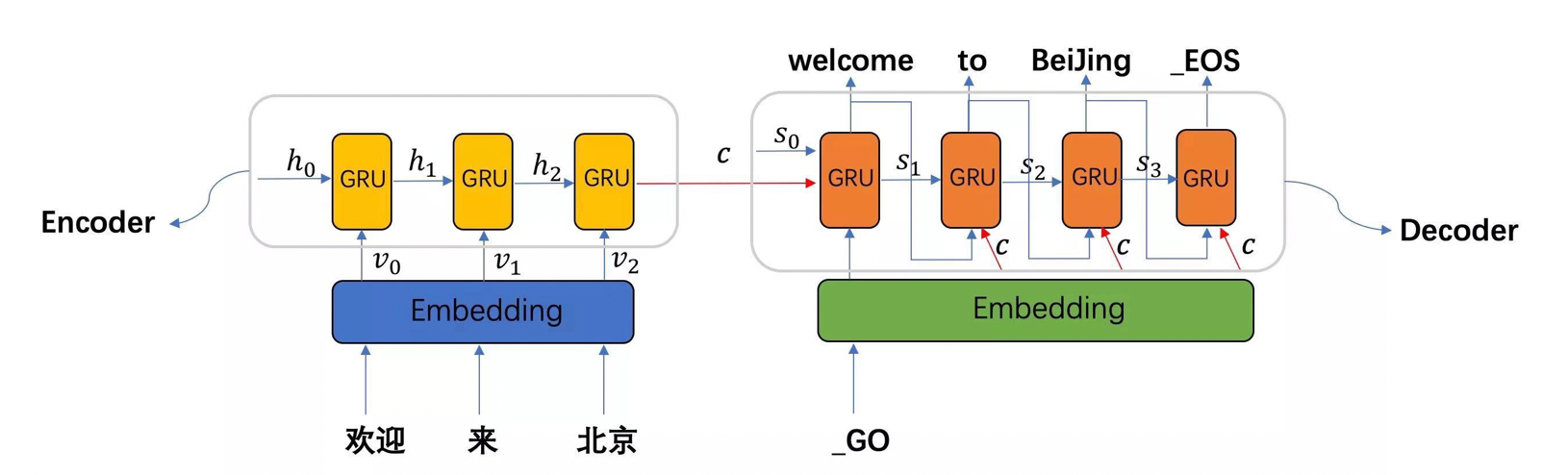
image.png

1）信息压缩困难，语义表达受限

2）缺乏动态感知，解码难以精准生成

3）并行效率低下

4）长距离的 “记忆” 差

3. Attention机制

3.1 transformer架构

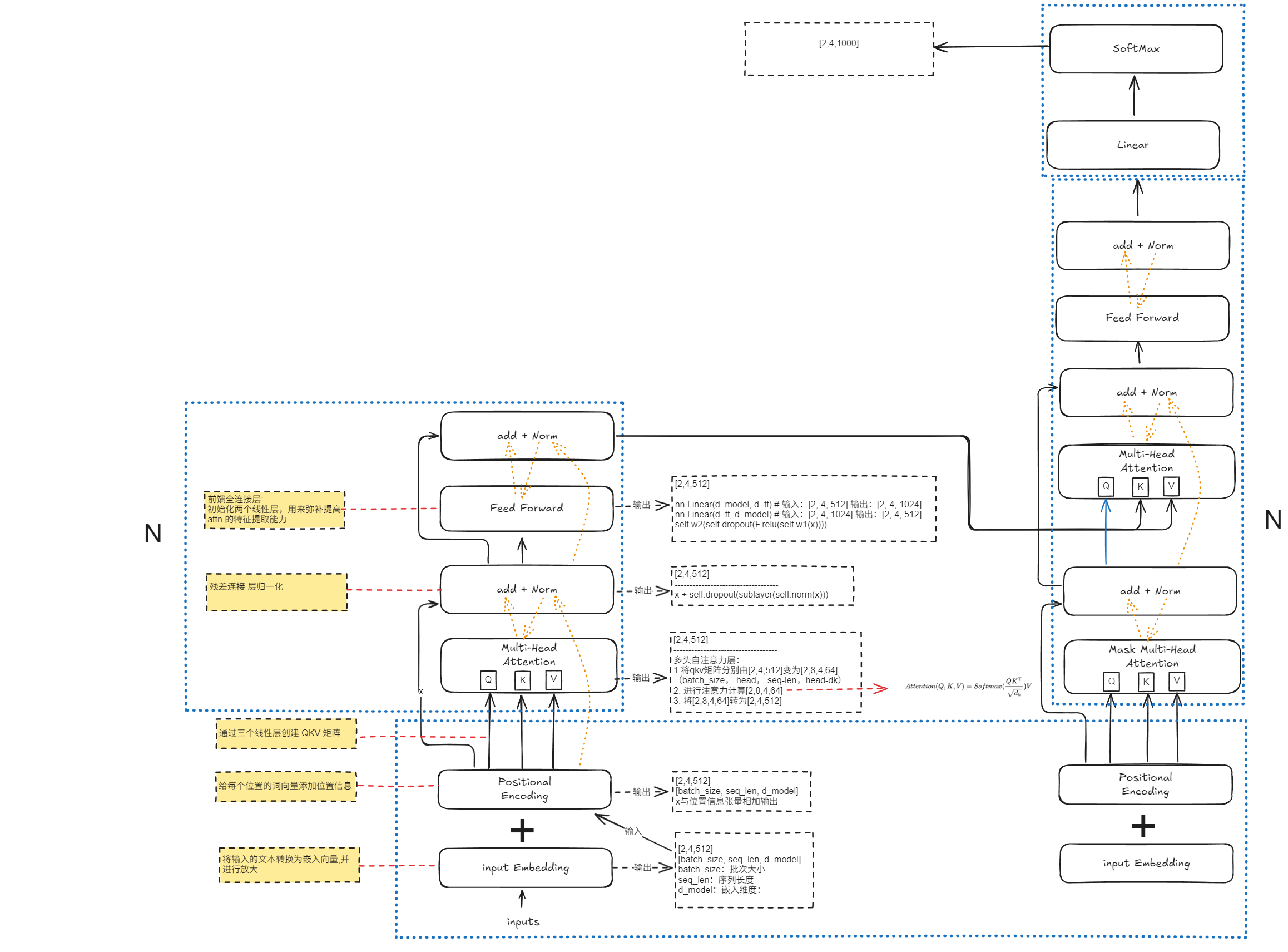
Drawing 2025-07-28 11.27.05.excalidraw.png

3.2 编码器自注意力层

transformer的核心就是自注意机制，本质是让模型能自主计算输入序列中每个元素与其他所有元素的关联权重，并基于权重 “聚焦” 关键信息。

假设输入句子是：[猫, 追, 狗, 它, 跑得, 很快]（已转换为词向量，每个词用一组数字表示） 为了计算 “谁和谁相关”，模型会先给每个词生成 3 个向量：

  • Q（Query，查询向量）：带着明确的目标（“找指代对象”）去探测其他词是否相关
  • K（Key，键向量）提供 可被 Q 识别的关联属性
  • V（Value，值向量）：该词所有与当前语境相关的核心信息

接下来，模型要算 “谁和谁更相关”，用的是Q 和 K 的点积（Dot Product）：
比如算 “它” 和 “狗” 的关联分，就是把 “它的 Q 向量” 和 “狗的 K 向量” 做数学上的点积（简单说，就是对应数字相乘再相加）。结果越大，说明两者越相关。

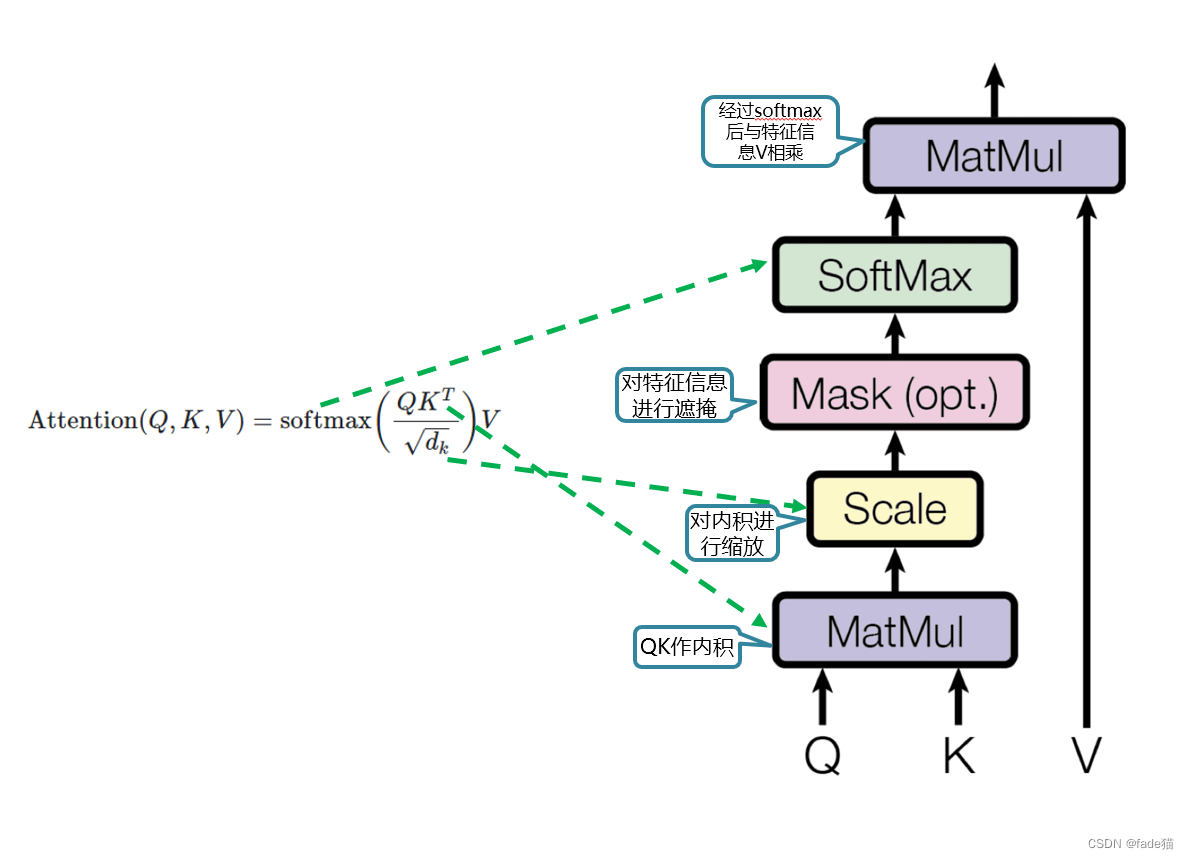
image.png

Query：“我要找什么” 的主动查询动作（比如 “找指代对象”“找相关动作的参与者”）。

Key：“我是什么 / 和什么相关” 的标签（比如 “我是追的主体”“我是被追的对象”），用于被 Q 匹配。

Value：“我包含的具体信息”（比如 “被追的狗的实体 + 状态”），用于被匹配后提供内容。

$$Attention(Q,K,V)=Softmax(Q⋅KT√dk)⋅V$$

需求：让序列中的每个位置（比如一个词），都能找到其他位置中和它最相关的词 Q_i= 位置 i 的需求向量（比如 [0.9, -0.2, 1.3]） K_j= 位置 j 的供给向量（比如 [0.8, 0.5, 1.1]） 怎么用一个数衡量 Q_i和 K_j的匹配度？​ 强烈需求 × 强大供给 = 大正数​​ → 高度匹配！ 弱需求 × 弱供给 = 小数​ → 低度匹配。

“自”注意力：Q = K =V，是因为模型在计算每个位置的表示时，所参考的信息全部来自同一个输入序列本身，而不是来自另一个序列。

假设一个迷你句子只有两个词：

  • ​​词A：“猫”​​（位置1）
  • ​​词B：“追”​​（位置2）
Q = [ [0.8, 0.2],   ← 猫的查询向量 Q_A      
      [0.3, 0.9] ]  ← 追的查询向量 Q_B

K = [ [0.7, 0.4],   ← 猫的键向量 K_A       
    [0.5, 0.6] ]  ← 追的键向量 K_B

我们需要一个 2x2 的结果矩阵，其中：

  • 第1行：词A（猫）对词A、词B的关联强度
  • 第2行：词B（追）对词A、词B的关联强度
Q × Kᵀ = [ [0.8, 0.2]   @   [0.7, 0.5] 
           [0.3, 0.9] ]      [0.4, 0.6] ]
           
S = [ [0.64, 0.52], # 猫对[猫, 追]的关联强度
[0.57, 0.69] # 追对[猫, 追]的关联强度 ]

Attn_Weights = [ [0.53, 0.47], # 猫的注意力分布：[对猫53%，对追47%]
					[0.47, 0.53] # 追的注意力分布：[对猫47%，对追53%] ]

词本身的特征v

V = [ [0.9, 0.1], # 猫的值向量 
	[0.2, 0.8] # 追的值向量 ]

权重 * v

S = [ [0.53, 0.47],    @ [ [0.9, 0.1],
[0.47, 0.53]              [0.2, 0.8]

[[0.53*0.9+0.47*0.2  ，0.53*0.1+0.47*0.8]
[0.47*0.9+ 0.53*0.2, 0.47*0.1+0.53*0.8]
python
'''
为什么除以根号dk：
     Q 和 K 的维度 dₖ很大（比如 512），直接计算点积 Q * Kᵀ会产生一个巨大的数值矩阵。这会带来两个严重问题：
    1、Softmax 的“梯度消失”问题​
        Softmax 函数对非常大的输入值极度敏感：
        输入值过大 → Softmax 输出概率会极端尖锐（比如某个位置概率≈1，其余≈0）。
        极端尖锐 → 梯度几乎为 0 → 模型无法更新权重（梯度消失）

    2、点积方差随维度爆炸性增长
        假设 Q 和 K 的每个元素是独立随机变量（均值为 0，方差为 1）：
        点积结果 Q * Kᵀ的方差 = dₖ（因为累加 dₖ个随机变量）。   数学定理推导出来的
        若 dₖ=512，方差扩大 512 倍 → 数值波动极大 → 训练震荡甚至发散

    具象化理解：
        假设 dₖ = 100：
        ​​不缩放​​：点积结果可能高达几千甚至几万，Softmax 输出几乎就是 “0 和 1” 的二值分布。
        ​​缩放后​​：点积结果除以 10（√100=10），数值回到几十的范围，Softmax 能输出有意义的概率分布（比如 [0.2, 0.7, 0.1]）。

    ​​√dₖ​​ 而不是其他值？
​          ​数学推导​​：若 Q、K 元素方差为 1，则 Var(Q*Kᵀ) = dₖ，缩放 1/√dₖ后方差变为 1，符合稳定需求
'''
def attention(query, key, value, dropout=None, mask=None):
    # 1 拿到dk
    d_k = query.size(-1) # 512
    # 2 缩放点积, scores.shape=(2,4,4) (bs, seq-len, deq-len)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)

    # 3 判断 mask
    # 作用：1、解码器端：实现解码的并行
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    # 4 进行softmax，拿到注意力权重
    p_attn = F.softmax(scores, dim=-1) # (2,4,4)

    # 5 判断dropout
    if dropout is not None:
        p_attn = dropout(p_attn)

    # 6 计算 attn @ V，并返回
    return torch.matmul(p_attn, value), p_attn # (batch_size, seq_len, d_model)

    # 2,4,4 @ 2,4,512 = 2,4,512

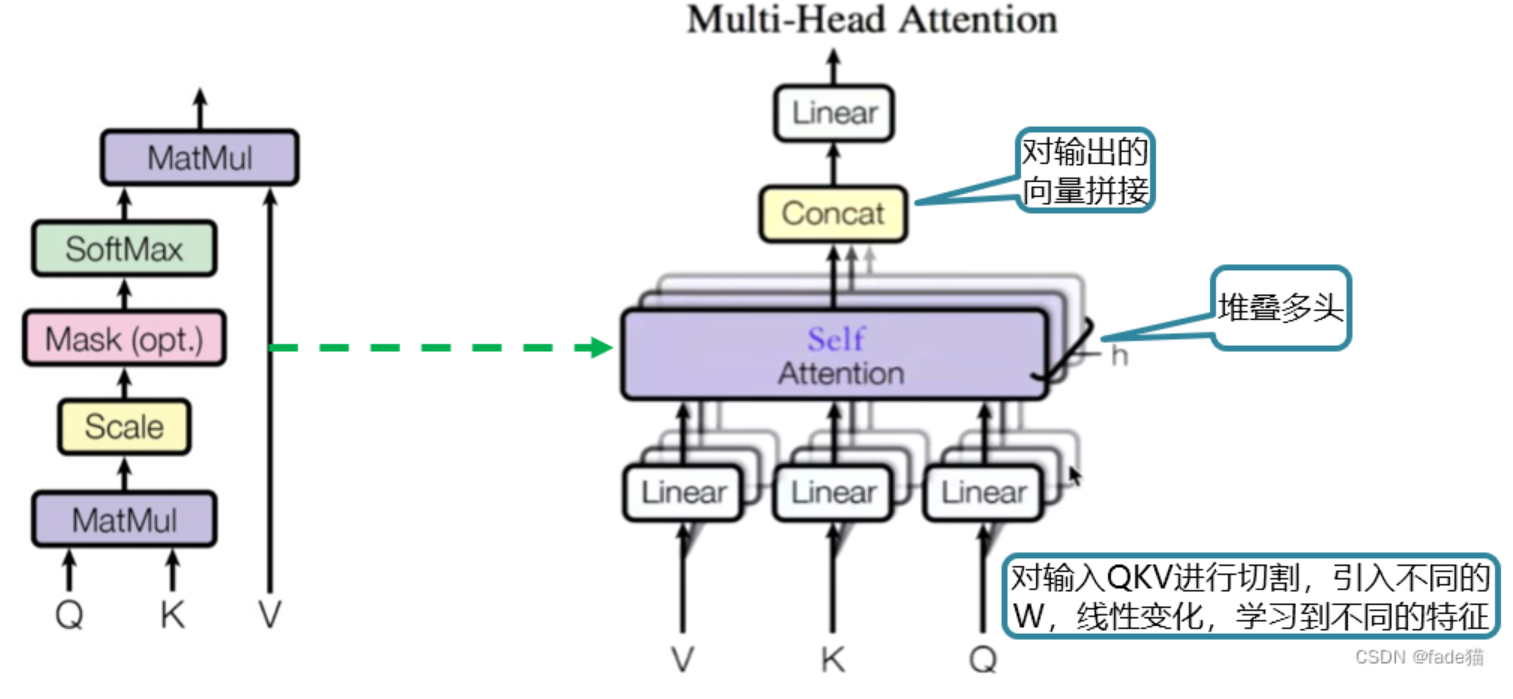
image.png

作用：让模型能够同时关注序列中不同位置的信息，并从多个不同的表示子空间学习词语之间的关系 ，从而更好地理解上下文语义和长距离依赖关系。

3.3 解码器自注意力层

掩码：让模型不要使用当前字符和后面的字符

解码器​​：需要​​逐个生成输出词​​（如逐步生成中文翻译）。 ​关键约束​*：在生成位置 i的词时，模型​​只能看到已经生成的 1 到 i-1位置的词​​，不能偷看未来的词（位置 >i）。

实现方式​​：在自注意力分数 (Q×Kᵀ) 之后、Softmax 之前，​​将未来位置的分数设为极小值（如 -∞或很大的负数）sentence_mask.png